Добрейшего времени суток, товарищи Форекс трейдеры! Чаще при оценке стратегий на Forex трейдеры смотрят на доходность в процентах. Чем их больше — тем лучше, не так ли? Но % доходности сильно зависит от риска и не отражает эффективности системы. Так какой показатель использовать? Стандартом у финансовых аналитиков считается Коэффициент Шарпа, выведенный нобелевским лауреатом Уильямом Шарпом.
Ниже мы рассмотрим как рассчитать коэффициент Шарпа для оценки эффективности стратегии, разберемся что же он означает (многие умеют его считать, но не понимают его смысла), а также сделаем выводы о том в каких случаях он полезен, а в каких нет.
Коэффициент Шарпа на Форекс
Коэффициент Шарпа придумал известный американский экономист – Уильям Шарп. На сегодня, это один из наиболее часто используемых показателей отношения риска к доходности. Еще большую значимость коэффициент приобрел, когда в 1990 году, за свою модель оценки финансовых активов (CAPM) Шарп был избран лауреатом Нобелевской премии.
Человеку из сферы финансов будет не сложно понять принцип расчета коэффициента Шарпа и что тот должен отображать. По сути, задача сводится к тому, чтобы узнать, сколько избыточной доходности вы получите в связи с удержанием более рискового актива. Думаю, не секрет, что лишний риск всегда должен сполна компенcироваться соответствующей доходностью. Чем больше значение коэффициента, тем больше прибыли на риск одной и той же суммы.
Формула расчета выглядит следующим образом:
Доходность актива
Доходность можно измерять с любой периодичностью – это может быть день, неделя, месяц, или год. Также, в качестве показателя доходности можно брать средний прирост на сделку. Единственное, желательно, чтобы исходные данные доходности должны быть нормально распределены. Отсюда и главная слабость коэффициента. Резкие пики на выборке в 3 и более стандартных отклонения и ассиметричное распределение (видимый наклон графика) могут стать причиной ложной оценки.
Безрисковый доход
Безрисковкый доход – это теоретический доход с нулевым риском. То есть, это та доходность, которую инвестор может получить абсолютно без риска за какой-то определенный период времени. По идее, — это минимальный доход, который инвестор ожидает получить от любой инвестиции. Сравнивая этот показатель с реальным доходом, можно определить, насколько хорошую компенсацию вы получаете за дополнительный риск.
На практике, понятия инвестиции с нулевым риском не существует, так как даже самые безопасные инвестиции несут с собой некоторую долю риска. Тем не менее, к безрисковой доходности можно отнести депозит в сбербанке, либо деньги, инвестированные в казначейские облигации США. Рынок форекс – это всегда инвестиции с высоким риском, поэтому безрисковая доходность в нашем случае будет равна нулю. Но, если ваш депозит хранится в банке, в формулу можно подставить значение текущей базовой ставки.
В терминале MT4 показатель Шарпа считается, как отношение среднеарифметической доходности сделки к стандартному отклонению, при нулевом значении безрисковой ставки.
Полная формула выглядит так:
Стандартное отклонение
Коэффициент Шарпа оценивает эффективность инвестиции с точки зрения дисперсии доходов. Так как мы уже подсчитали избыточную доходность (доходность за вычетом безрисковой ставки), осталось поделить это значение на стандартное отклонение доходности актива. То есть, посчитать отношение доходности к риску.
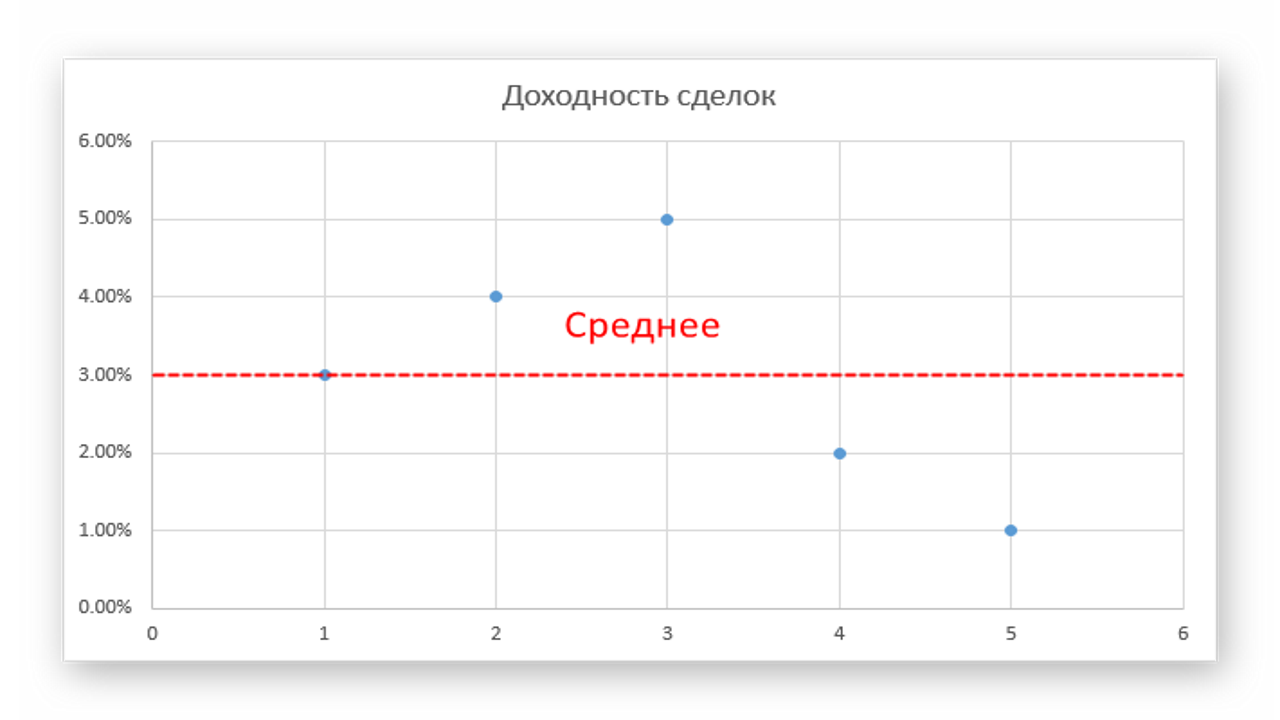
Хотя сегодня это уже и не требуется, все же стандартное отклонение несложно рассчитать вручную. Допустим, вы собрали небольшую статистику доходности сделок: 3%, 4%, 5%, 2%, 1%. На первом этапе мы вычитаем из этой последовательности среднее и получаем такой ряд: 0%, 1%, 2%, -1%, -2%.
Далее, возводим значения в квадрат, получаем арифметическое среднее и выводим корень от результата – sqrt((0.00% + 0.01% + 0.04% + 0.01% + 0.04%) / 5) = 1.41%.
Для сравнения, возьмем немного другую выбрку: 2%, 8%, 5%, 4%, 6%. Очевидно, что доходность такой системы в рамках рассматриваемого периода больше, но мы также наблюдаем гораздо большую волатильность доходности, 2% против 1.41% у предыдущего примера. Соответственно, первая стратегия является менее рискованной.
Единицы расчёта коэффициента Шарпа
Для примера, попробуем сравнить эффективность двух торговых стратегий по показателям их доходности и риска. Допустим, первая стратегия дает 5% прибыли на сделку, при стандартном стандартном отклонении (показатель дисперсии доходности) равном 4%. Вторая стратегия в среднем приносит по 2% в каждой сделке, но отклонение не превышает 1%. В данном случае, первая стратегия будет иметь коэффициент шарпа 1.25, а вторая – 2.0. Это означает, что не смотря на меньшую доходность, вторая стратегия имеет лучшее соотношение риска к доходности.
Коэффициент Шарпа должен быть равен одному или выше. Тогда считается, что стратегия, которую мы анализируем, работает с достаточной эффективностью. Значение больше трех уже говорит о том, что вероятность получения убытка в каждой сделке меньше 1%. И чем больше полученное значение, тем лучше.
Вывод
В большинстве случаев, коэффициент Шарпа покажет реальную рентабельность стратегии. Но, иногда, показатель Шарпа может вводить в заблуждение. Например, некоторые облигации могут показывать стабильную доходность выше банковского процента в течении многих лет, на что коэффициент ответит нереалистично высокими показателями. В этом случае, полученное значение ничего не скажет о реальных рисках, стоящих за инвестированием в данную облигацию, пусть даже риск будет на самом деле минимальным. В целом же, данный коэффициент подойдёт для сравнения двух стратегий с относительно частыми входами и не самыми огромными целями.
С уважением, Алексей Вергунов
TradeLikeaPro.ru
