Вы наверняка уже многое слышали о мартингейле, сетках и прочих зрелищных способах слить ваш депозит. И действительно, это такие системы, которые даже чисто теоретически не позволят вам выигрывать постоянно. Тем не менее, существует множество трейдеров, в том числе и опытных, которые используют сетки на своих счетах. Думаете, они не знают теорию? Конечно же знают, просто тут есть небольшой секрет. И о нем мы и будем сегодня говорить.
Дело в том, что большинство частных трейдеров имеют довольно скромные счета и очень часто они выбирают достаточно агрессивные методы управления капиталом. Сетки и мартингейлы действительно довольно часто приводят к потерям всего депозита, но опытные трейдеры всегда советуют периодически снимать часть заработанного. И таким образом, мы получаем более-менее стабильный заработок на, казалось бы, даже чисто теоретически сливающих торговых системах. И сегодня мы узнаем, почему же так происходит с математической точки зрения и научимся извлекать из этого «чуда» максимум полезного.
Что такое вероятность разорения
Этот самый «чудесный способ» зарабатывать на сливающих стратегиях можно вполне использовать с научным подходом, достаточно ознакомиться с таким понятием, как вероятность разорения.
Зная вероятность разорения для конкретной торговой системы с выбранным методом мани менеджмента можно более-менее точно сказать, сольется ли трейдер, или нет. Очень многие трейдеры, особенно начинающие, вечно куда-то спешат, как будто рынки скоро закроют и они не успеют наторговать свои миллионы на безбедную жизнь. В итоге вероятности их разорения зашкаливают и, как результат – очередной слитый счет.
Вероятность разорения, или probability of ruin, сокращенно POR, — это статистическая вероятность того, что система торговли доведет счет до разорения прежде, чем будет достигнут долларовый уровень, который считается удачным. Разорение определяется по уровню счета, когда трейдеры остановят торговлю. POR иллюстрирует трейдерам статистическую возможность того, что их системы торговли сдвинутся к успеху или разорению.
Некоторые авторы считают, что интерес к вероятности разорения неуместен, так как она не дает трейдерам представление о том, как получать прибыль. В этом смысле они правы. К тому же вероятность разорения имеет тенденцию быть маленькой величиной в реально зарабатывающих системах торговли. Однако, если все другие аспекты равны в своем значении, то, делая выбор между двумя системами торговли, вы, скорее всего, выберете ту, у которой самая низкая вероятность разорения.
Чаще всего, у долгосрочно зарабатывающих систем риск разорения достаточно мал. Редко когда он доходит до отметки в 5%. Как правило, это системы торговли, которые имеют достаточный капитал и приносят прибыль трейдеру. У новичков нередко можно встретить POR в районе 70-100%, что говорит о том, что счет обязательно будет слит, даже если они говорят вам, что наконец нашли граальную систему торговли. POR величина непостоянная и у нормальных трейдеров она большую часть времени держится в пределах от 0 до 5%. Но если вы видите, что этот показатель возрос, скорее всего вы стали слишком сильно рисковать. В этом случае достаточно просто снизить риски в каждой сделке, и тогда вероятность разорения вернется на приемлемый уровень.
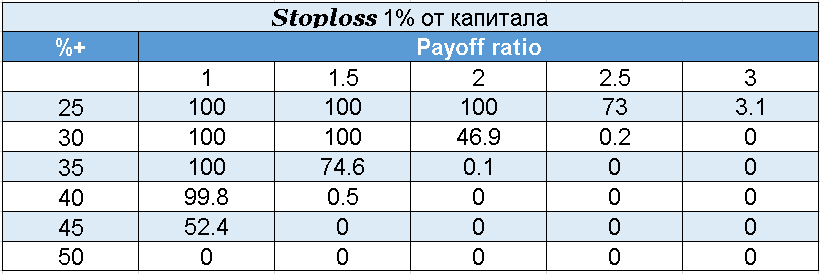
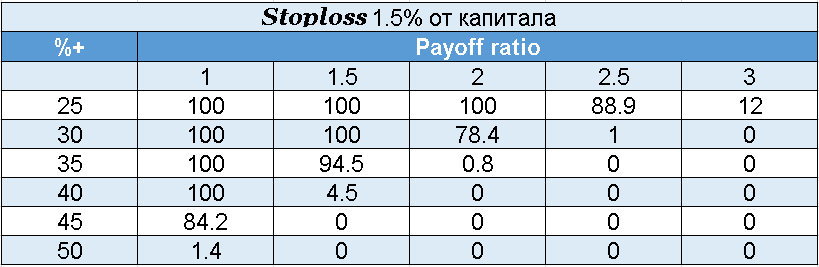
Ниже вы можете увидеть риски разорения при использовании жестких стопов. Для расчета учитывается вероятность выигрыша в каждой сделке и отношение прибыли к убытку.
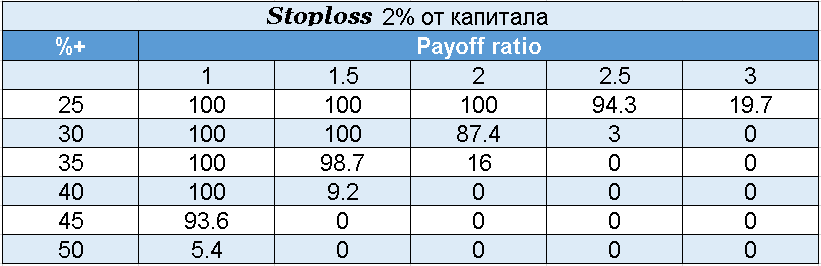Важно учесть, что стопы для расчета брались фиксированными, а вероятность получения выигрышной сделки была неизменна во времени, хотя в реальности это, конечно же, не так.
Формула расчета
Приведу простейшую формулу для вычисления вероятности разорения:
Где q — вероятность «неудачи», убыток от которой в каждом отдельном испытании равен -1;
р — вероятность «успеха», прибыль от которого в каждом отдельном испытании равна +1.
Q(z = 0) — вероятность разорения, наступающего тогда, когда начальный капитал (z) становится равным 0. Тогда P(w) = 1 — Q(z = 0) — это вероятность достижения цели (увеличение начального капитала (z) до величины w).
Как видите, в ней не учитывается величина выигрышей и проигрышей. То есть такую формулу можно применять только к таким системам, у которых выигрыши всегда равны проигрышам.
Давайте рассмотрим пример. Мы имеем 100 баксов, и наша система дает 45% прибыльных сделок. Тогда q = 0,55 и р = 0,45. Мы хотим узнать, с какой вероятностью мы сможем данной системой достичь 100% прибыли, или 100 долларов прибыли.
Q = ((0,55/0,45)^200 – (0,55/0,45)^100)/((0.55/0,45)^200-1) = 99,(9)%, то есть практически 100%.
И вероятность успеха P(w = 100) = 1 — Q(z = 0) = 0. Нулевая вероятность успеха означает однозначный слив депозита еще до того, как будет достигнуто 100% прибыли.
Тем не менее, оказывается, что если в качестве цели поставить получение выигрыша лишь одного доллара, то вероятность добиться успеха в этом составляет:
P(w = 100) = 1 — Q(z = 0) = 0,818 или почти 82%.
Соответственно, какой плохой ни была бы система, чем больше начальный капитал трейдера, тем значительнее шансы выиграть малую сумму до того, как он разорится. Даже при неблагоприятной вероятности успеха в каждой отдельной попытке шансы у трейдера выиграть малую сумму до того, как он разорится, могут быть значительными. И они тем выше, чем больше начальный капитал.
В этой связи интерес представляет более детальная оценка изменения вероятности разорения в зависимости от постепенного увеличения ставки в неблагоприятных условиях (q > р). Опуская математические выкладки, отметим, что при неизменности начального капитала постепенное увеличение ставки приводит к уменьшению вероятности разорения обреченного трейдера. Соответственно, вероятность разорения для того, кому успех обеспечен по математическому ожиданию, увеличивается.
Это также можно сформулировать так: в повторяющейся игре с постоянной ставкой вероятность разорения будет минимальной при выборе такой ставки, которая была совместимой с суммой желаемого выигрыша.
Например, у нас есть z = 90 долларов, а хотим мы получить w = 100 при тех же вероятностях q и p.
Q = ((0,55/0,45)^100 – (0,55/0,45)^90)/((0.55/0,45)^100-1) = 0,866 или 87% вероятность потерять депозит.
Но если увеличить ставку до максимально возможного значения (в данном примере нам нужно 10 долларов и z = 9, w = 10), то столь неблагоприятный прогноз может сильно измениться.
Q = ((0,55/0,45)^10 – (0,55/0,45)^9)/((0.55/0,45)^10-1)= 0.21
И хотя математическое ожидание выигрыша остается тем же, вероятность разорения составит всего лишь 0,21, а выигрыша — возрастет до 0,79.
Как видим, несмотря на неблагоприятные соотношения р и q, у обреченного трейдера есть значительные шансы выйти победителем в какой-то из попыток. Разумеется, эту победу можно сохранить лишь тогда, когда трейдер имеет возможность удалиться из торговли со своим выигрышем.
Еще более простая формула получается для испытаний с идеальной монеткой, когда p=q=50%:
Q(-z) = 1 — (z/w),
где (w — z) > 0 — «чистый» выигрыш.
Тогда вероятность такого исхода:
P(z) = 1 — Q(-z) = z/w.
Если исследовать зависимость функции Q(z/w) от соотношения переменных z и w и построить график, то обнаруживается следующее:
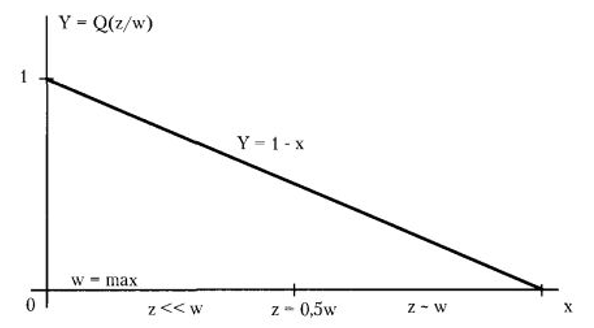При некотором заданном постоянном значении z (z = const) вероятность разорения уменьшается по мере изменения величины w в сторону сближения с z. И вероятность разорения достигает минимальных значений, когда величины w и z становятся сравнимыми (z — w).
При р = q вероятность разорения Q становится минимальной, а выигрыша Р — максимальной при двух условиях. Это минимальная цель выигрыша и максимальная ставка.
Например, при ставке 0.1 z мы получим w = z + 0.1z и Q(-z) = 0.09, а вероятность выигрыша 91%.
Давайте рассмотрим еще один пример. Пусть игрок имеет начальный капитал в $3000. Ставка (stoploss = takeprofit) при каждой игре составляет $300. Тогда имеем условия: z = 3000 и w = 3300. Но поскольку в качестве «условной единицы» служит величина $300, то в масштабе исчисления, использованного выше, это означает, что z = 10, а w = z + 0,1z = 11. И мы приходим к условиям и решениям предыдущего примера, где: Q(-z) = 0,09 и P(w) = 0,91.
Давайте теперь рассмотрим пример с установкой на счет бота-мартышки. Думаю, всех интересует наиболее сильно именно этот пример. У нас есть 1000$ и мы поставим эксперта на депозит с сотней долларов. Наша первостепенная задача – вывести первые 100% прибыли, после которой мы в случае дальнейшего слива будем при своих. В таком случае z =100% (наши 1 000), а w = 110% — нам нужно получить прибыль 10% от начального депозита. Тогда можно записать так: z = 10, w =11. Предположим, что мы не знаем будущего и будем считать, что с одинаковым успехом можем проиграть нашу ставку в 100 долларов и выиграть 100% от нее. То есть, в среднем, в половине случаев мы будем сливать наши счета. Тогда:
Q(-z) = 1 — (z/w) = 1 – 10/11 = 0.09, или 9% шанса остаться без денег. При этом шанс оказаться с 1 000$ на руках и прибылью 100$ составляют 91%.
Если хотя бы в 60% случаев мы не проиграем нашу сотню, что будет означать, что мы получили весь страховочный депозит обратно и у нас работает бот с сотней, которую нам уже не жалко потерять, то вероятность будет уже намного выше:
Q = ((0,4/0,6)^11 – (0,4/0,6)^10)/((0.4/0,6)^11-1)= (0,01156 — 0,01734)/( 0,01156 — 1) = 0.00585, или 0,6% риска разорения. Тогда вероятность получения прибыли будет 99,4%.
Чтобы лучше понять этот подход, давайте возьмем теперь начальный капитал 400 долларов, а p=q=0.5. Тогда z = 3, а w = 4:
Q(-z) = 1 — (z/w) = 1 – (3/4) = ¼ = 0.25, или 25% вероятность потери всех средств до того, как мы успеем вывести сотню. После этого с вероятностью 75% у нас на руках будет снова наши 400 долларов и 100 долларов будут работать на депозите с мартышкой. Что дальше? Дальше можно просто снимать прибыль с этого счета и не переживать за то, что счет когда-нибудь сольется. Ведь в этом случае вы останетесь при своих и просто повторите цикл с начальным капиталом в 400 долларов.
Математическое ожидание
Как видим, при неблагоприятном соотношении р <q можно, управляя значениями w, z и размером ставки, добиться впечатляюще хороших пропорций Q(z) и P(w).
В этой связи возникает вопрос о том, каково математическое ожидание результата, т.е. средний выигрыш в ходе продолжительного повторения игры, при условиях неблагоприятного соотношения р < q и благоприятного соотношения Q(-z) < P(w).
Как следует из условий, конечный результат игры («победа» w или «поражение» z = 0) — это случайная переменная, которая принимает одно из двух значений: (w-z) или (-z).
Тогда математическое ожидание выигрыша М для любого, в том числе и равного, соотношения q и р:
М = P(w) * (w — z) — Q(z = 0) * (-z) = w x P(w) — z.
А при q = p:
М = w * (1-Q(z = 0))-z.
Если в эти формулы подставить значения Q(z = 0), то получим:
М (для q > р) < 0
и
М(q = р) = w X {1 — Q(z = 0)} — z = w X (z/w) — z = 0.
Знание этих расчетов позволяет выбирать «наименьшее зло». Таким образом, необходимо учитывать следующее важное правило: если трейдер находится в неблагоприятных условиях р < q и ставит задачу закончить либо после того, как выиграет сумму w, либо проиграет предельно допустимую сумму z, то никакие соотношения Q(-z) < P(w) не изменят негативного математического ожидания результата.
Итак, никакие манипуляции с указанными переменными не позволяют рассчитывать на положительное значение математического ожидания. Хуже того, недостижимым является даже ноль.
Таким образом, порядок применения рационального способа управления случаем может быть следующим: для заданного соотношения р и q проводится расчет конкретного варианта соотношения величин w и z, при котором достигается максимальное математическое ожидание («наименьшее зло»). Для заданных р и q стоит выбирать такие соотношения переменных w и z, которые обеспечивают наилучшее математическое ожидание. Однако напомним, что речь идет о математическом ожидании результата при условии бесконечного числа испытаний.
В этой связи полезно рассмотреть оценки средней продолжительности игры, при которой, согласно теории вероятностей, могут быть достигнуты заранее установленные цели. И данный параметр продолжительности также следует принимать во внимание в процессе управления.
Средняя продолжительность
Приведем без вывода основные формулы оценки средней продолжительности игры для разных соотношений р и q.
Для случая, когда q не равно р (р> q или р <q) и при размере исходного капитала z, а цели w (в каждой игре ставка составляет одну условную единицу), решение уравнения приводит к формуле:
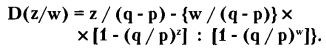Вернемся к приведенному выше примеру, в котором существует положение «невыгодной» игры при q = 0,55 и р = 0,45 (z = 90, w = 100 «условных единиц»). Мы уже видели, что если при каждом испытании ставка будет равной одной «условной единице», то вероятность разорения Q(z) = 0,866. Тогда вероятность выигрыша P(z) = 0,134.
По формуле расчета средней продолжительности игры получим, что ее математическое ожидание при этом составит:
D(z/w) = 767 испытаний.
Однако если увеличить ставку до максимальной, сделав ее равной 10 «условным единицам», то соответственно получим:
Q(z) = 0,210, a P(z) = 0,790.
И математическое ожидание продолжительности игры:
D(z/w) = 11 испытаний.
Соответствующее правило можно сформулировать так: чем меньше математическое ожидание продолжительности игры, тем вероятность выигрыша при «невыгодном» соотношении q>p становится все более благоприятной.
Чем меньше ожидаемая продолжительность «невыгодной» игры, тем лучше. Этот расчет отвечает закону больших чисел: чем больше число испытаний, тем ближе будут результаты к математическому ожиданию вероятности «успеха».
Для q = p действительна другая формула, которая имеет вид:
D(z/w) = z x (w- z).
Сразу отметим, что средняя продолжительность игры оказывается значительно выше, чем это подсказывает нам «здравый смысл».
Так, если q = р, то при исходном капитале z = 90 условных единиц и желании игрока довести эту сумму до w = 100:
D(z = 90 / w = 100) = 90 х 10 = 900.
Заметим, что при ставке в 10 «условных единиц» вероятность «успеха» весьма высока:
P(z = 90 / w = 100) = 90 / 100 = 0,9.
Однако потребуется немало времени, чтобы получить тот или иной результат (разорение или «чистый» выигрыш в 10 единиц).
Даже если игрок ставит столь скромную задачу, как «окончательный выигрыш» всего одной «условной единицы» (w = z + 1), то продолжительность игры при капитале z = 90:
D(z = 90 / w = 91) = 90 х 1 = 90.
При этом вероятность «успеха» предельно благоприятна:
P(z = 90 / w = 91) = 90 / 91 = 0,99.
Обратим внимание на то обстоятельство, что, несмотря на высокую вероятность выигрыша, предстоит долгая борьба (в среднем 90 испытаний). И это для того, чтобы получить выигрыш, равный всего одной единице капитала.
Однако утешает то, что «условная единица» капитала может составить значительную сумму «живых» денег. Правда, тогда придется задействовать начальный капитал, который в 90 раз больше выигрыша.
Как видим, невозможно заранее задать наиболее «выгодный» путь: многое зависит от разных обстоятельств.
Вернемся к приведенному выше примеру, но в качестве одной «условной единицы» примем $300.
Тогда случайная величина D(w/z) с учетом новой «единицы» вычисляется по формуле:
D(w/z) = (z / 300) х (w — z) / 300.
Рассмотрим ожидаемую продолжительность игры в зависимости от того, какие цели ставит трейдер.
При желании выиграть $300, т.е. 10% от исходного капитала, получим следующие оценки:
— вероятность выигрыша:
P(z = 3000 / w = 3300) = z / w = 3000 / 3300 = 10/11 = 0,91;
— продолжительность игры:
D(w = 3300 / z = 3000) = (z / 300) х (w — z) / 300 = 10.
Сравним этот результат с другими условиями.
Если целью ставится увеличить капитал на 20% при той же ставке $300 в каждой игре:
— вероятность выигрыша:
P(z = 3000 / w = 3600) = 10/12 = 0,83;
— продолжительность игры:
D(w = 3600 / z = 3000) = 20.
Для двукратного «обогащения» при тех же условиях:
— вероятность выигрыша:
P(z = 3000 / w = 6000) = z / w = 0,5;
— продолжительность игры:
D(w = 6000 / z = 3000) = 200.
Таким образом, приведенные расчеты вновь подтверждают полученные уже ранее оценки: чем более масштабными являются цели, тем менее вероятным становится их достижение.
При этом продолжительность игры возрастает быстрее, чем интуитивно предполагается. В приведенном примере видно, что увеличение размера цели от 20 до 100% (в пять раз) увеличивает среднюю продолжительность игры с 20 до 200 испытаний (в десять раз).
Увеличение цели по прибыли при прочих равных условиях ведет к снижению вероятности выигрыша и непропорционально большому возрастанию продолжительности игры.
Ну и напоследок давайте рассчитаем ожидаемую продолжительность для нашего примера с установленными на счета ботами-мартышками. Итак, у нас 400 долларов начального депозита и мы кладем по 100 долларов каждый раз на счет. Вероятность проиграть все деньги достаточно велика: Q(-z) = 1 — (z/w) = 1 – (3/4) = ¼ = 0.25. D = 3/(4-3) = 3, то есть в среднем подобный исход будет достигаться за 3 ставки.
Главные выводы (для тех кому лень читать формулы и расчеты)
Вероятность разорения не так уж необходима для трейдеров, которые торгуют, используя классические системы управления капиталом. Если трейдер рассчитывает риск разорения, можно определить, не слишком ли сильно он рискует в данный момент, а также не слишком ли маленький капитал у него для начала торговли по новой системе.
Самую значимую пользу от этого знания могут получить трейдеры, торгующие при помощи опасных систем и советников. Состоит она в том, что вы можете рассчитать риск разорения при серии запусков опасных советников, ожидаемую от этого прибыль, количество попыток в серии и вероятность при этом разориться. Я, конечно, не призываю ринуться устанавливать опасные советники на ваши счета, но если вы и так этим занимаетесь, то предлагаю воспользоваться более научным подходом, чем игра в казино.
Не углубляясь в вышеперечисленные формулы, хотелось бы несколькими простыми словами еще раз сказать о пользе вычисления вероятности разорения.
- Итак, имея 1000 долларов и опасный советник, который хотя бы в половине случаев не сливает ваш депозит, а позволяет снять первую прибыль в 100% и рискуя при этом 100 долларов за раз, вы с вероятностью 91% отобьете ваши вложения. Если ваш советник чаще позволяет заработать, вероятность повышается практически до 100%.
- Если у вас в запасе всего 400 долларов, а советник требует не менее 100 за раз, при этом расклад по прежнему 50 на 50, вы останетесь без своих денег с вероятностью 25%. При этом, если вы будете повторять эту процедуру множество раз, в среднем вы каждый будете выходить в плюс после третьей попытки (то есть, например, первый раз проиграли 100 и осталось 300, второй раз выиграли 100 и остались при своих, третий раз все получилось и у вас на руках все вложенное, плюс 100 долларов на счете с советником).
Заключение
Если вы не против различных математических расчетов, можно довольно просто рассчитать стратегию для управления капиталом для опасных советников — начальный капитал, среднее количество попыток и математическое ожидание вашей стратегии. Если же формулы наводят на вас скуку — просто воспользуйтесь расчетами, которые были приведены в этой статье в качестве примеров. Все эти данные и выкладки ведут к одному очень простому правилу — для безопасного запуска опасного бота нужно иметь начальный капитал в 10 раз превышающий требуемый под советник депозит. Это позволит нам практически гарантированно получить обратно наши вложения и, возможно, начать получать прибыль.
С уважением, Дмитрий аkа Silentspec
TradeLikeaPro.ru
